Two – Dimensional Array
-
Two
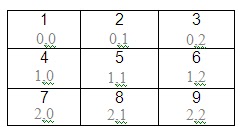
dimensional arrays consist of number of rows and columns.
-
Two
dimensional arrays are commonly referred as matrix.
Declaring two
dimensional array
data-type
array-name[rows][cols];
|
e.g.
int x[3][3];
x[3][3]={{11,22,33},{44,55,66},{77,88,99}};
The
first value is at x[0][0]=11, x[0][1]=22…………….. x[2][2]=99.
If
you watch carefully then you will notice that every cell has two subscripts
(index/location values). So you can access these locations by using nested for
loop. Outer loop is for rows and inner for columns.
Let
us clear this by using simple program.
//scan
& print elements of matrix
#include<stdio.h>
#include<conio.h>
void
main()
{
int x[3][3],i,j;
clrscr();
printf("\nEnter elements of x
matrix");
for(i=0;i<3;i++)
{
for(j=0;j<3;j++)
{
scanf("%d",&x[i][j]);
}
}
printf("\nElements of x matrix");
for(i=0;i<3;i++)
{
for(j=0;j<3;j++)
{
printf("%d\t",x[i][j]);
}
printf("\n");
}
getch();
}
o/p:
Enter
elements of x matrix
1
2
3
4
5
6
7
8
9
Elements
of x matrix
1 2
3
4 5
6
7 8
9
In
case of transpose of matrix rows and columns are interchanged.
Program
to print transpose of matrix
//program
to scan & print elements of matrix
#include<stdio.h>
#include<conio.h>
void
main()
{
int x[3][3],t[3][3],i,j;
clrscr();
printf("\nEnter 3 x 3 elements of matrix:
");
for(i=0;i<3;i++)
{
for(j=0;j<3;j++)
{
scanf("%d",&x[i][j]);
}
}
//process
for(i=0;i<3;i++)
{
for(j=0;j<3;j++)
{
t[i][j] = x[j][i]; //
columns and rows of x copy to rows and columns of t
}
}
printf("\nTransposed elements of x
matrix: ");
for(i=0;i<3;i++)
{
for(j=0;j<3;j++)
{
printf("%d ",t[i][j]);
}
printf("\n");
}
getch();
}
o/p:
Enter
3 x 3 elements of matrix:
1 2 3
4 5 6
7 8 9
Transposed
elements of x matrix:
1 4 7
2 5 8
3 6 9
//prog
to print sum of rows, columns and all elements of matrix
#include<stdio.h>
#include<conio.h>
void
main()
{
int x[3][3],i,j;
int rsum=0,csum=0,sum=0;
clrscr();
printf("\nEnter elements of x matrix:
");
for(i=0;i<3;i++)
{
for(j=0;j<3;j++)
{
scanf("%d",&x[i][j]);
}
}
//process
for(i=0;i<3;i++)
{
for(j=0;j<3;j++)
{
sum = sum + x[i][j];
rsum = rsum + x[i][j];
csum = csum + x[j][i];
}
printf("\nSum of row = %d",rsum);
printf("\nSum of column =
%d",csum);
rsum=0;
csum=0;
}
printf("\nSum of all elements =
%d",sum);
getch();
}
o/p:
Enter
elements of matrix:
1
2
3
4
5
6
7
8
9
Elements
of x matrix
1 2
3
4 5
6
7 8
9
Sum
of row = 6
Sum
of column = 12
Sum
of row = 15
Sum
of column = 15
Sum
of row = 18
Sum
of column = 24
Sum
of all elements = 45
Square
matrix has two diagonals 1st and 2nd respectively. You
can perform process on it. Here the next program is to print sum of 1st
and 2nd diagonal.
//sum
of 1st & 2nd diagonal
#include<stdio.h>
#include<conio.h>
void
main()
{
int x[4][4],i,j,dsum1=0,dsum2=0;
clrscr();
printf("Enter 4X4 elements of x
mat\n");
for(i=0;i<4;i++)
{
for(j=0;j<4;j++)
{
scanf("%d",&x[i][j]);
}
}
//process
for(i=0;i<4;i++)
{
for(j=0;j<4;j++)
{
if(i == j) //In case of 1st diagonal the indices of row and
column are
same hence whenever this condition becomes true then elements of 1st
diagonal will add to dsum1
{
dsum1 = dsum1 + x[i][j];
}
if(i+j == 3) //In case of 2nd
diagonal the sum of indices of row and column is
less by 1 of given size hence whenever this condition becomes true then
elements of 2nd diagonal will add to dsum2
{
dsum2 = dsum2 + x[i][j];
}
}
}
printf("\nSum
of 1st diagonal = %d",dsum1);
printf("\nSum
of 2nd diagonal = %d",dsum2);
getch();
}
o/p:
Enter
4X4 elements of x mat
1
2 3 4
4
5 3 2
2
3 3 2
7
6 2 3
Sum
of 1st diagonal = 12
Sum
of 2nd diagonal = 17
Here
you have to see one more type of sum i.e. triangle sum. Square matrix has upper
and lower triangle. If you have matrix as follows
Look
at above matrix the elements(1,2,3,5,6) locate under upper triangle and others
are elements of lower triangle. Then now think of how to access elements to
calculate sum of upper and lower triangle.
If
you watched carefully then i=j will find that in case of upper triangle the
index i is less than or equal to j and in case of upper triangle opposite
position is appeared.
Let
us check this logic through a program below:
//prog
to cal. sum of upper & lower triangle of matrix
#include<stdio.h>
#include<conio.h>
void
main()
{
int x[4][4],i,j,upp=0,low=0;
clrscr();
printf("\nEnter 4X4 elements of x
matrix\n");
for(i=0;i<4;i++)
{
for(j=0;j<4;j++)
{
scanf("%d",&x[i][j]);
}
}
printf("\n4X4 elements of x
matrix\n");
for(i=0;i<4;i++)
{
for(j=0;j<4;j++)
{
printf("%d\t",x[i][j]);
}
printf("\n");
}
for(i=0;i<4;i++)
{
for(j=0;j<4;j++)
{
if(i <= j) //upper
triangle
{
upp = upp + x[i][j];
}
if(i >= j) //lower
triangle
{
low = low + x[i][j];
}
}
}
printf("\nSum of elements of upper
triangle = %d",upp);
printf("\nSum of elements of lower
triangle = %d",low);
getch();
}
o/p:
Enter
4X4 elements of x matrix
1
1
1
1
2
2
2
2
1
1
1
1
3
3
3
3
4X4
elements of x matrix
1 1
1 1
2 2
2 2
1 1
1 1
3 3
3 3
Sum
of elements of upper triangle = 15
Sum
of elements of lower triangle = 20


No comments:
Post a Comment